Delaunay 三角形分割

Delaunay三角形分割とは

「平面上の点の凸胞を周囲とし、各三角形の角の最小値が最大(MaxMin)でかつ最適な分割」。
「最適」とは最小角が等しい場合、次に小さい角がより大きい方を「最適」という。4点(以上)が同一円周上にあるとき、最小角は分割の仕方にかかわらず同じであるが、、理論上は4点が同一円周上にはないとして議論をすすめる。
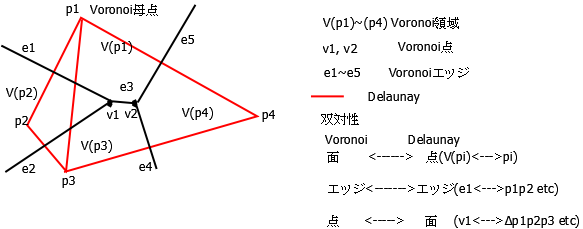
これと同値の定義として、「Delaunay三角形分割はVoronoi図の双対」、「各三角形の外接円の内部に他の点を含まない三角形分割」がある。
「Voronoi図」とは、平面上の各点(Voronoi母点)からの距離が他の点からの距離より短い点の集合をVoronoi領域といい、そのVoronoi領域の境界線(Voronoiエッジ) と交点(Voronoi点)からなる図である。そしてVoronoiエッジを共有する母点(Voronoi近傍)を結んでできるのが「Delaunay三角形分割」である。

「Delaunay分割はVoronoi図の双対」->Voronoi図の一意性->Delaunay分割の一意性(もちろん4点以上が同一円周上にはない)。

Delaunay作成アルゴリズムの基礎(Hjell and Dæhlen[1]chap3)

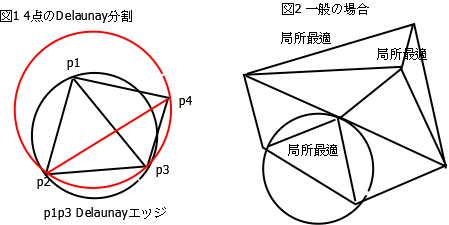
4点が同一円周上になく凸四角形をなすとき、Delaunay分割は一意的に決定されることは容易にわかる(Δp1p2p3の外接円がp4を含まない。図1)。
一般の4点以上の三角形分割で、境界上のエッジ、内部のエッジでそれを対角線にもつ四角形が凹の場合、また凸四角形でDelaunayエッジ、これらを局所最適(locally optimal) という(図2)。
あるエッジが局所最適かどうかは、それを対角線とする四角形だけで判定すればよい。
そして、「全てのエッジが局所最適の三角形分割はDelaunay分割である」([1]p66)。

アルゴリズム-逐次添加(Hjell and Dæhlen[1]chap4)

1点づつ既存のDelaunay分割に付け加えていき、全てのエッジが局所最適(Delaunay分割)になるようにする。

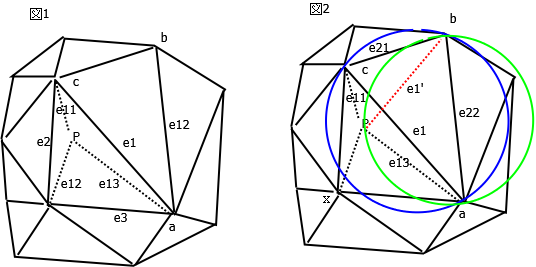
挿入点pとそれを含む三角形の頂点を結んで三角形分割する(図1)。
- 図1でe1, e2, e3だけ局所最適がどうか調べる。局所最適でなければもう一方のエッジと交換する。
- e11, e12, e13は局所最適(凹四角形)。
一般にエッジ交換するとそれを対角線とする四角形の４辺が局所最適の判定候補になるが、実際は「外側」だけのエッジだけ判定すればよい(図2)。
- 図2でe1-->e1'と交換したとき、判定対象としてe11, e13, e21, e22が考えられるが、実際は「外側」e21, e22だけを調べればよい([1]p84)。

挿入点を含む三角形の決定と局所最適の判定方法

座標系は右手系とする。

平面上の3点P1(x1,y1), P2(x2, y2), P3(x3, y3)に対して

F(P1,P2,P3)= 1 x₁ y₁ 　

1 x₂ y₂

1 x₃ y₃

とすると、P1,P2,P3がこの順序で反時計回りのとき>0、時計回りのとき<0である。よって3点P1, P2, P3が反時計回りで点pがその中にあるときは、 F(p,P1,P2)>0, F(p,P2,P3)>0, F(p,P3,P1)>0である。
(局所最適判定)4点P1(x1,x2), P2(x2,y2), P3(x3,y3),P4(x4,y4)について、

G(P1,P2,P3,P4)= 1 x₁ y₁ x₁²+y₁² 　

1 x₂ y₂ x₂²+y₂²

1 x₃ y₃ x₃²+y₃²

1 x₄ y₄ x₄²+y₄²

とおくと、
P1,P2,P3が反時計まわりとした時、三角形P1P2P3の外接円に関するP4の位置は、G(P1,P2,P3,P4) > 0 のとき外部、 = 0 のとき円周上、 < 0 のとき内部にある(杉原[2])。

「整数帰着法」、「記号摂動」(杉原[2])

"float"や"double"など浮動小数点で計算すると誤差が問題になる。それを解決するため、全ての数を桁数の多い整数(多倍長)で表すのが「整数帰着法」である。問題になるのが多倍長どうしのかけ算で、普通のやり方ではできない。ただ、かけ算ぐらいは自前でプログラムでできそうだし、サイトをあたればライブラリもいくつか見つかる。
実際の場面では「挿入点が既存のエッジの上にくる(共線)」、「既存の点と重なる」、「4点が同一円周上にある」などの「退化」が発生する。プログラムによってはいろいろ例外処理をおこなうが、プログラムを理解しづらくするし、「完璧」になるとは限らない。
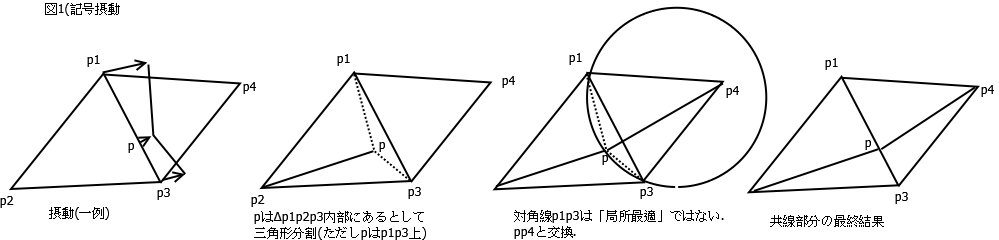
「退化」を処理する1つの方法が([2]第2章)「記号摂動」である。これは(自分なりの理解では)点を「ウェート」に応じて無限小移動させて「退化」を解消するものである。「ウェイト」のつけ方はいくつかあるが、[2]では初期入力の段階で順序が早いほうが「高く(大きく移動)」、同じ点ではx座標が一番「高く」、次はy座標、z座標の順である。そして上の行列式も補正され、「退化」を解消する(図1)。

改訂版補足

改訂版では、浮動小数点数(double)で上のF(P1,P2,P3) とG(P1,P2,P3,P4) を計算する。その場合どの時点で「記号摂動｣を使うのかが問題になる。G(P1,P2,P3,P4) で考えると、これは実質的に3次の行列式で、その誤差評価式が杉原[2]p209に載っている(<=18d/10⁶)。ただし、それはfloatの場合なので、 doubleの仮数部を52ビットとすれば、3次の行列式の誤差は、< = 18d/2⁵²(と思うが?)。 dは3個の座標の積(絶対値)の最大値(このプログラムではd=1となる)。

G の計算では、doubleでの計算が20/2⁵²より小さいとき(20は2次以上の誤差まで考えて)、記号摂動を使う。
F の計算では、doubleでの計算が 10/2⁵²より小さいとき(2次行列式の誤差は< 6d/2⁵²と思うが?)、記号摂動を使う。

Delaunay [逐次添加法」は最初、与えられた点を取り囲む四角形を形成し、その四角形を2つの三角形に分割して、そこに1点、1点付け加えて作っていく。最後にその四角形の4頂点から出発している三角形を消去しなければならない。ただし、そのまま消去したのでは凹んだところが出てくる。この凹みを埋めていく作業がある。そのとき、外郭の凹凸判定は、F を使ってもよい(前のプログラムはそうしていた)が、今回はオリジナルの crossProduct2d(NewTraits.h)を使った。これは、ベクトルの外積のz成分を計算するものである。

参考

Ø.Hjell and M.Dæhlen Triangulation and Applications. Springer-Verlag 2006
杉原厚吉 FORTRAN 計算幾何プログラミング. 岩波書店 1998

G(P1,P2,P3,P4)=	1	x₁	y₁	x₁²+y₁²
	1	x₂	y₂	x₂²+y₂²
	1	x₃	y₃	x₃²+y₃²
	1	x₄	y₄	x₄²+y₄²