順序数空間の直積空間 (ω_0+1) × (ω_1+1) × (ω_2+1) ×・・・ について教えて下さい.
順序数空間の直積空間
(ω_0+1) × (ω_1+1) × (ω_2+1) ×・・・
から1点 (ω_0, ω_1, ω_2,・・・) を取り除いた空間 S が擬コンパクトであることの理由を教えて下さい.
ここで,空間 X が擬コンパクトであるとは,
X 上の任意の実数値連続関数が有界であることを意味します.
お答えします:
空間 S が稠密な可算コンパクト部分空間
D=(ω_0+1) × ω_1 × ω_2 ×・・・
を含むからです.
ご回答まで.
距離関数 d_1, d_2, d_∞ に関する開集合がそれぞれ互いの開球の和として表されるとは,どのような意味ですか.
退職して趣味で数学をしています.
距離関数 d_1, d_2, d_∞ からできる開集合系は同じとのことで,
お互いに開球の和集合で表されるとのことですが,具体的イメージがわきません.
お答えします:
ご質問の中の「開球」とは,距離空間の点の「ε-近傍」のことを意味します.
『はじめよう位相空間』の補題 8.9 をご覧下さい.
距離空間 X の任意の開集合 U をとると,任意の点 x ∈ U に対して,
U(x) ⊆ U を満たす x の ε-近傍が存在します.
すべての点 x ∈ U に対して,このような U(x) をとると,
U はこれらの U(x) の和集合と一致します.
すなわち,距離空間の任意の開集合は開球の和集合として表現されます.
この事実を,ご質問の場合に当てはめると,次のことがわかります.
距離空間 (R^n, d_1) の開集合は d_1 に関する開球の和集合として表される.
距離空間 (R^n, d_2) の開集合は d_2 に関する開球の和集合として表される.
距離空間 (R^n, d_∞) の開集合は d_∞ に関する開球の和集合として表される.
ここで,以上の3つの距離空間の開集合は同じなので,それぞれ,互いに他の距離関数に
関する開球の和集合として表されることがわかります.
具体的イメージが湧いたでしょうか?
定理 9.1 の条件 (2) だけを証明する方法を教えて下さい.
都内の某私立大学数学科の2年生です.
集合と位相という科目,特に位相分野で初っ端から非常に苦戦しております.
『はじめよう位相空間』の定理 9.1 に関する証明です.
定理 9.1 任意の写像 f: X ---> Y に対して,次の3条件は同値である.
(1) f は連続写像である.
(2) Y の任意の開集合 U に対し,f^{-1}(U) は X の開集合である.
(3) Y の任意の閉集合 F に対し,f^{-1}(F) は X の閉集合である.
ここで,条件 (2)「Y の任意の開集合 U に対し,f^{-1}(U) は X の開集合である」 だけを証明するには,どのようにすればよいのでしょうか?
お答えします:
条件 (2) だけを証明することは出来ません.
(2) の主張「Y の任意の開集合 U に対し,f^{-1}(U) は X の開集合である」は,
これだけでは真偽が定まらないからです.
等式「x + 3 = 0」の真偽が定まらないことと同じです.
しかし,「任意の位相空間 X, Y と任意の写像 f: X ---> Y に対して,条件 (1) と (2) が同値である」ことは証明できます.
この場合,X と Y と f が「任意の」という全称記号で束縛されたので命題になったからです.
詳しくは,『はじめよう位相空間』の 2.4 節をご覧下さい.
実際に,そのことを証明した定理が,定理 9.1 であると言えます.
位相で苦戦しておられるとのこと,授業だけで理解することは難しいので,
ご自分で勉強されることが大切と思います.
私は3年生のとき,自分で本を読んで初めて少し分かった気になりました.
K.N.さんの勉強が進むことを祈っています.
2017/3/8 改
距離空間において,全体集合と空集合は開かつ閉集合でしょうか.
迅速にご回答下さりありがとうございました.
丁寧に解説して下さったため,該当箇所について理解できました.
しかし,その後,読み進めるうちにまた新たな疑問が出てきたので質問させていただきます.
前に質問させて頂いた定理の証明の後に,開集合の定義が書いてありました.
その定義とは,
「距離空間 (X, d) の部分集合 A の補集合 A^c が閉集合であるとき,Aを開集合という」
というものです.
この定義から,次の定理が導かれると書いてありました.
定理. 距離空間 (X, d) の開集合に関して,次の性質が成り立つ.
X および空集合 φ は開集合である.
証明は省かれていましたが, 距離空間 (X, d) の開集合における全体集合 X の補集合 X^c は φ となるため、 前の定理より φ は閉集合であるから,X は開集合といえる. ということで証明ができると考えました. その場合,ここでの全体集合 X は開集合になります.
私が疑問に思ったのは,
この定理から求められる全体集合 X は,
前の定理から求められる全体集合 X と意味が違ってくるのではないか,ということです.
つまり,前の定理から求められた全体集合 X は閉集合であったが,
距離空間 (X, d) の開集合においては,
全体集合 X は開集合であったため,
距離空間 (X, d) が閉集合か開集合かで全体集合 X が違う意味合いになってしまうのではないか,
ということです.
もし,全体集合 X が同じものであれば,「全体集合 X は開集合でありかつ閉集合である」.
また,「空集合 φ も開集合でありかつ閉集合である」といえると思うのですが,
いかがでしょうか.
お答えします:
その通りです.
T.M.さんの推論は正しいと思います.
任意の距離空間 X において,全体集合はつねに X を意味します.
そして,全体集合 X は X の開集合でありかつ閉集合です.
また,空集合 φ も X の開集合でありかつ閉集合です.
余計なことですが,開集合 (open set) であると同時に閉集合 (closed set) でも ある集合を,英語では clopen set ということがあります. 日本語には,適当な用語がありません. 任意の距離空間 X において,X と φ は clopen sets です.
疑問は解決したでしょうか.
取り急ぎ,回答まで.
距離空間において,全体集合と空集合が閉集合であることの証明について教えて下さい.
来年から経済学の大学院に進学するにあたり, 数学の準備として集合と位相に関する勉強を進めています. 経済学部生用のテキストの中で1つ疑問に残っている点が出てきたため, 質問をさせていただきます. 距離空間に関するものです. その部分をまず教科書から抽出します.
定理.距離空間 (X, d) の閉集合に関して次の性質が成り立つ.
X および空集合 φ は閉集合である.
証明.
全体集合 X の数列 {x_n} の極限点 x_0 は X の元であるから,
「X = X の閉包」がいえる.
空集合 φ はいかなる元も含まないからその数列の極限点の全体も空集合であり,
「φ = φ の閉包」がいえる.
と書いてありました.
私が質問したいのは証明の部分です.
証明の最初に,全体集合 X の数列 {x_n} の極限点 x_0 は X の元であるから,と言っていますが,
これは距離空間 (X, d) の閉集合という前提の上から言えるのでしょうか?
私は,距離空間 (X, d) の閉集合であっても,その中に含まれる全体集合 X は必ずしも閉集合とは限らないのではないか,という疑問を持ちました.
お答えします:
任意の距離空間 (X,d) において,全体集合 X は閉集合です.
距離空間の閉集合の定義には,いろいろな方法がありますが,
ご質問の箇所は,次の定義に基づいて証明がなされています.
以下,(X, d) を X と略記します.
距離空間 X の部分集合 A が X の閉集合であるとは,
A が次の条件 (*) を満たすことをいう.
(*) X の任意の収束する点列 {x_n} と その極限点 x_0 ∈ X に対し,
もし,すべての n について x_n が A の点ならば,x_0 も A の点である.
A = X のとき,この条件が満たされているかどうか考えてみて下さい.
もともと x_0 は X の点ですから,A = X なら (*) が満たされます.
ゆえに,X は X の閉集合です.
A = φ の場合は,(*) の中の文章
「すべての n について x_n が A の点ならば,x_0 も A の点である」
について考えてみましょう.
このとき,前半の仮定の部分が偽なので,論理の規則から,
この文章自体は常に真になります.
ゆえに,空集合 φ も X の閉集合です.
いかがでしょうか.
T.M.さんの疑問は,閉集合の定義の理解の仕方に原因があるように 思いましたので,ていねいに書いてみました.
大学院への勉強が進むことを祈っています.
回答まで.
例 5.7:数式 (5.1) はどのように導くのですか?
『はじめよう位相空間』
を読んでいて分からない点がありまして,質問させてください.
例 5.7 の (5.1) の式の導き方を教えていただけないでしょうか.
よろしくお願いします.
お答えします:
写像 f は,S^1 - {p_0} 上の点 p を,p と p_0 を結ぶ直線が x 軸と交わる点へうつします
(図 5.3 をご覧下さい).
したがって,S^1 - {p_0} 上の点 p = (x, y) をとり,
まず,点 p と p_0 = (0, 2) を結ぶ直線の方程式を求めます.
次に,この直線と x 軸との交点の座標を求めると,
f(p) = 2x/(2 - y) が得られます.
是非,ご自分で計算してみて下さい.
S さんの勉強が進むことを祈っています.
連結成分の具体例を示して下さい.
いつもお世話になり有難うございます.
連結成分のことですが,
『解いてみよう位相空間』の 153 ページの問題 8.2 で,
集合 S = {a, b, c} 上の連結な位相構造は,例えば,
T_18 = {φ, {b}, {c}, {b, c}, S}
です.
このとき連結成分は何になるでしょうか?
連結成分について,何か具体的な例を示していただければ有難いのですが.
よろしくお願いいたします.
お答えします:
位相空間 X が与えられたとき,X の各点 x に対して,
x を含むすべての X の連結集合の和集合 C(x) を X の連結成分と言います.
232 ページの問題 12.9 より,C(x) は連結集合です.
また,2つの連結成分は,一致するか交わらないことが分かります.
このことは,連結成分全体の集合が X を分割することを意味しています.
具体例を考えてみましょう.
上の位相空間 (S, T_18) の場合:
点 a を含む連結集合は,{a}, {a, b}, {a, c}, S.
ゆえに,C(a) = {a} ∪ {a, b} ∪ {a, c} ∪ S = S.
点 b を含む連結集合は,{b}, {a, b}, S.
ゆえに,C(b) = {b} ∪ {a, b} ∪ S = S.
点 c を含む連結集合は,{c}, {a, c}, S.
ゆえに,C(c) = {c} ∪ {a, c} ∪ S = S.
以上により,(S, T_18) の連結成分は S だけです.
一般に,連結空間 X の連結成分は X になります.
次に,位相
T_8 = {φ, {a}, {b, c}, S}
の場合を考えてみましょう.
位相空間 (S, T_8) は連結ではありません.
点 a を含む連結集合は,{a} だけ.
ゆえに,C(a) = {a}.
点 b を含む連結集合は,{b}, {b, c}.
ゆえに,C(b) = {b} ∪ {b, c} = {b, c}.
点 c を含む連結集合は,{c}, {b, c}.
ゆえに,C(c) = {c} ∪ {b, c} = {b, c}.
以上により,(S, T_8) の連結成分は {a} と {b, c} です.
連結成分が,X を分割していることが分かると思います.
最後に,位相
T_24 = {φ, {a}, {b}, {a, b}, {b, c}, S}
について,位相空間 (S, T_24) の連結成分を求めてみて下さい.
答えは,{a} と {b, c} です.
M さんの勉強が進むことを祈っています.
導集合の導集合の包含関係が縮小して行くとは,どういう意味ですか?
退職して趣味で数学をしていますが,色々と不明な点がでできます.
よろしくお願いいたします.
導集合の導集合の意味が判りません(集積点の集積点).
また「導集合の導集合の包含関係が縮小していく」とは,どういう意味でしょうか?
お答えします:
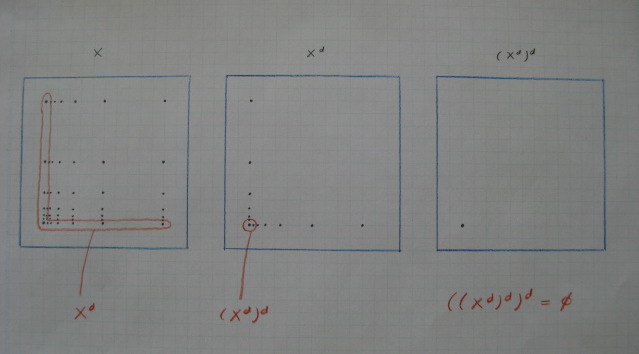
位相空間 X の集積点の集合を導集合とよび,X^d で表します.
導集合の導集合 (X^d)^d は,部分空間 X^d の集積点の集合です.
くどくど説明するよりも,典型的な例を考えると,一目瞭然と思います.

上の図は,極限点 0 を含めた収束列
S = {0} ∪ {1/2^n : n ∈ N}
の直積集合 X = S × S について考えています.
左図は,X の導集合(=集積点の集合)を赤で囲んで示しています.
中図は,X^d の導集合を赤で囲んで示しています.
すなわち,(X^d)^d は原点1点だけからなる集合です.
左図は,(X^d)^d = {(0,0)} です.
この図形は集積点を持たないので,導集合は空集合です.
すなわち,包含関係
X ⊇ X^d ⊇ (X^d)^d ⊇ ((X^d)^d)^d = φ
が成立します.
この事実を「導集合の導集合の包含関係が縮小していく」と言います.
いかがでしょうか.
連結性と局所連結性の違いについて教えて下さい.
退職して趣味で数学をしていますが,いろいろと不明な点がでできます.
お時間をとって申し訳ないのですが,よろしくお願いいたします.
『解いてみよう位相空間』の 238 ページの例について,
連結であるが局所連結でないと他の本で書いていました.
局所連結と連結の違いがよく判りません.
「平面上でふたつの交わらない開円板を描き,それを合わせたものをXとすれば,それは連結でないが局所連結である」とか「関数 f(x) = [x}(ガウス記号)のグラフ G(f) は平面 R^2 おいて局所連結である」など,局所連結の意味が判りません.
連結性と局所連結性の違いについて教えて下さい.
お答えします:
位相空間 X のすべての点 p が,次の条件 (LC) を満たすとき,X は局所連結であるという.
(LC): 点 p の任意の近傍 V に対して,U ⊆ V を満たす p の連結な近傍が存在する.
M さんが言われる通り,この定義はわかり難いところがありますので, 平面上の図形を使って, 「連結であるが局所連結でない空間」の例 X と 「局所連結であるが連結でない空間」の例 Y を与えたいと思います.
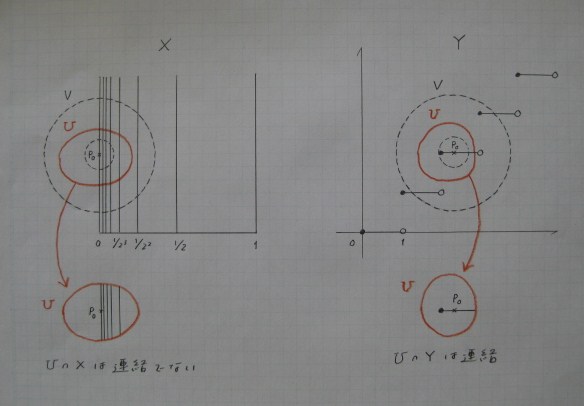
上の左図は,平面 R^2 の図形
X = {(x, 0) : 0 ≦ x ≦ 1} ∪ {(0, y): 0 ≦ y ≦ 1} ∪ {(1/2^n, y) : n ∈ N, 0 ≦ y ≦1}
です.
このとき,点 p ∈ X の X における近傍は,
平面 R^2 の p を含む開集合と X の共通部分であることに注意して下さい.
最初に,X は全体がつながっているので連結です.
ところが,図の点 p_0 = (0, 1/2) は条件 (LC) を満たしません.
なぜなら,ε< 1/2 である p_0 の ε-近傍 V (=大きい点線)をとると,
V は連結な近傍を含まないからです.
実際,図のように,p_0 を含む任意の開集合 U に対して,
もし U ∩ X ⊆ V ならば,U ∩ X は連結ではありません.
一方,上の右図の図形 Y は,関数 f(x) = [x] のグラフです.
図形 Y は連結ではありませんが,どんな近傍 V(=大きな点線)をとっても,
図のように開集合 U をとると,U ∩ Y は連結です.
したがって,Y は局所連結になります.
メールでご説明することには,限度があるのですが,
上図の図形 X, Y は典型的な例です.
よく比較されると,連結性と局所連結性の違いが分かるのではないでしょうか.
回答まで.
学部数学は暗記ですか?
はじめまして. 現在,工学部に在学していますが,数学の厳密さに引かれ数学系の大学院に進学しようと思い勉強しています. トポロジーがやりたく思っています.
そこで質問なのですが,表題の通り学部数学は暗記(暗記の比重がかなり多い)ような気がしていて, モチベーションが上がらないのですが,そこは諦めて苦行と思ってやるしかないのでしょうか.
先生の著書の
『はじめよう位相空間』と
『解いてみよう位相空間』を両方購入させていただいたのですが,
定義についてもう諦めて単語帳のようなものを作って通学時間に見ています.
ただ気がかりなのは,例えば連結であることを証明する際に「連結でないと仮定すると…」と始めて,背理法を用いておられます.他の書籍でも全てそうですし,数学科の友人も演習の時間にそう教わったそうです.
私はなぜ定義に戻って証明できないのかが気になりますし,もしそれができないのであればそれを証明して欲しいです.
このようないわゆるテンプレートを知らないとなかなか解答できないタイプの問題が多すぎる気がするのです.
他にも定義に戻ると証明が困難か不可能で,同値の命題を利用することがあります.
同値なのだからそれを使えば良いというのは当然ですが,知らないと自力で命題を思いついて証明して更に使わなければいけなくなるので難易度に天と地ほどの差が発生します.
良い訓練にはなるとは思いますが,特に定理など過去の偉人が産みの苦しみで着想したものを全て一からというのは不可能ですし,目先の院試を突破することを目標に設定すると,結局は覚えないと仕方ないと思うのです.
逆に知っていれば作業になってしまい,あまり面白くありません.
受験数学だと,例えば図形ならベクトルを使う,平面幾何を使う,座標を設定するなどできますから,自由度が高いように思います.
研究レベルになると,様々な方法で縦横無尽に数学の世界を駆け巡ることができるのであれば,このような苦行にも耐えますし,覚悟はしています.
この点について,先生のご意見をお聞かせ願えないでしょうか.
また諦めてやりましょうということであれば,問題のテンプレートを仕入れる方法を教えていただけないでしょうか.
今のところは,「幾何,演習」などで検索したり,大学院への演習などを入手,購入しています.
お忙しいところ恐縮ですが,お返事いただけると幸いです.
よろしくお願いいたします.
お答えします:
的確な答えが難しいのですが,内容を拝見して,感じたことを書いてみたいと思います.
学部数学は暗記ですか?との問いですが, 学部でも大学院でも,「受験のための勉強」を除けば,そうではないと思います.
テキストを読んで,十分理解した上で,出来るだけ正確な自分のノートを作って,もし忘れても,必要なときにはそれを見れば分かるようにするというのが,私の勉強法です.
しかし,受験の際には忘れたからと言ってノートを見ることが出来ません.
また,限られた時間内に解答を書かなければなりません.
すなわち,数学の勉強において,「受験のための勉強」は,特殊なものだと言えるのはないでしょうか.
T.N.さんはトポロジーを研究したいと書いておられます.
また,学部数学は暗記ような気がしていてモチベーションが上がらないとも書いておられます.
もしそうなら,受験のことを考えずに,十分に時間をかけてトポロジーの勉強に取り組まれてはどうでしょうか.
それが研究の第一歩だと思います.
そのように勉強をされれば,きっと多くのことを自然に覚えると思います.
覚えることと暗記は違います.
大学院受験を心配されるかも知れませんが,もし不合格なら,また,翌年受験すればよいではありませんか.
大切なことは,自分のしたい勉強をすることであって,大学院進学は,その1つの手段に過ぎないのではありませんか.
私は23才のときに修士課程を受験しましたが,口頭試問の時に,「たとえ不合格でも,大学院のゼミには参加させてほしい」とお願いしました.
勉強の形はいろいろあると思います.
背理法についての後半のご質問ですが,上に書いたような勉強に取り組まれたら,必ずご自分で答えが見つかると思います.
その日が早く来ることを祈っています.
以上,私が思ったことを書きました.
取り急ぎ,お返事まで.